Ultraschall-Entfernungssensor HC-SR04
Einige Fakten rund um das Thema
Bluepill, STM32F103C8T6 (ARM®32-bit Cortex®-M3 CPU)
Blackpill, STM32F411CEU6 (ARM®32-bit Cortex®-M4 CPU)
Messung der Laufzeit-Differenz
Transmitteranzahl, μC-abhängig
Beispielprojekte
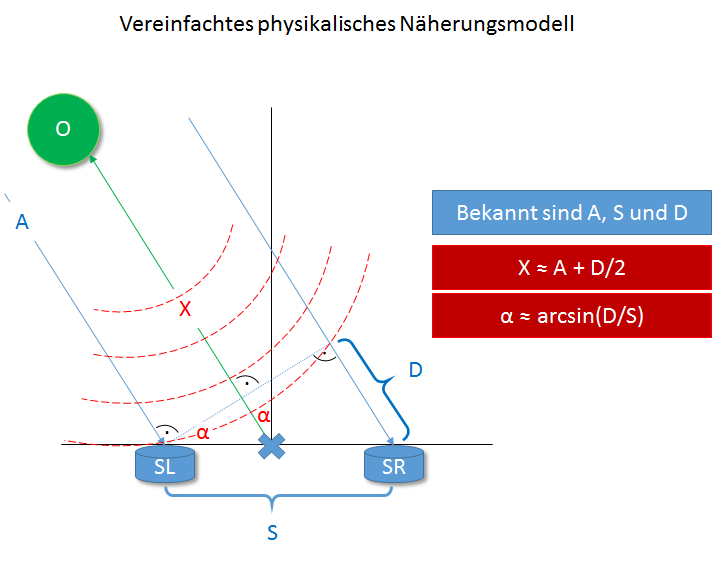
Bei Hackster.io gibt es das Projekt Spread Spectrum Phased Array Sonar. Hier geht es darum nach dem Prinzip einer Phased-Array-Antenne durch den gleichzeitigen Einsatz von zwei Ultraschall-Entfernungsmessern vom Typ HC-SR04 nicht nur die Entfernung zu einem Objekt, sondern auch dessen Richtung zu bestimmen. Das ganze sieht dann so aus:
Projekte mit ähnlichen Inhalten sind hier zu finden:
-
Virtual touch screen (3D Ultrasonic Radar)
Das Funktionsprinzip ist leicht zu verstehen. Die verschieden Eingangskanäle werden zeitverzögert überlagert (Interferenz). Setzt man die Zeitverzögerung in Relation zu der Sendefrequenz bzw. zur Wellenlänge, entspricht die Zeitverzögerung einer Phasenverschiebung. Die Phasenlage, die die höchsten Amplituden ergibt, gibt Hinweise auf die Richtung des reflektierenden Objekts.
- Sound Camera
- MicLoc
- SonicSurface: Phased-array for Levitation
- benwang.dev/2023/02/26/Phased-Array-Microphone.html
- DIY sonar scanner (practical experiments) Ein Vidoe von bitluni's lab. Und https://www.youtube.com/watch?v=Evao3XUUAOY.
- HC-SR04: Aufbau und Funktion
- Ultrasonic “radar”: Reflections from multiple targets
- Richtschall mit Ultraschall (Elektor)
Ultraschall-Entfernungssensor HC-SR04
In beiden Projekten werden immer komplette Ultraschall-Messer verwand, wobei jeweils nur ein Sendeteil aktiv ist. Bei emil habe ich einen Schaltplan des HC-SR04 gefunden und eine Anleitung, wie man das Ganze optimieren kann.
 |
 |
| Original | Optimiert |
Die Idee ist nun die Steuereinheit und das Sendeteil nur einmal zu bauen und die Empfangseinheit mehrfach auf einer Platine anzuordnen, wobei die US-Empfänger sehr genau positioniert werden können.
Eine sehr detaillierte Analyse des HC-SR04 findet man unter http://www.pcserviceselectronics.co.uk/arduino/Ultrasonic/index.php.
Andere Ansätze
Lösung von Alex Toussaint: How I built an ultrasonic 3d scanner
Einige Fakten rund um das Thema
Die Schallgeschwindigkeit in Luft beträgt etwa c=343 m/s.
Ein US-Signal mit der Frequenz von f = 40 kHz hat eine Wellenlänge in Luft von λ = c / f ≈ 0,86 cm. Die Dauer einer Schwingung beträgt 0,025 ms = 25 µs.
Der Original SR-HC04 sendet 8 Wellenzüge (Rechteck). Die Gesamtlänge dieses Wellenzugs ist 8 × λ ≈ 7 cm. Die Dauer, die der gesamte Wellenzug zum passieren eines Punkts benötigt, beträgt 8 × 25 µs = 200 µs.
Die Laufzeit des Signal bei Reflektion durch ein Objekt hängt von der Schallgeschwindigkeit ab: t = s / c.
| Entfernung | Laufzeit einfach |
Laufzeit hin & zurück |
|---|---|---|
| 50 cm | 1,5 ms | 2,9 ms |
| 100 cm | 2,9 ms | 5,8 ms |
| 150 cm | 4,4 ms | 8,7 ms |
| 200 cm | 5,8 ms | 11,6 ms |
| 300 cm | 8,7 ms | 17,4 ms |
| 400 cm | 11,6 ms | 23,3 ms |
| 500 cm | 14,6 ms | 29,0 ms |
Die Reichweite des HC-SR04 beträgt nominal 400 cm. Hierbei ist die Frage ob der interne Prozessor Impulse nach etwa 25 ms nicht mehr auswertet oder ob die Signale bei größeren Entfernungen zu schwach werden um den internen Komparator zu triggern.
Exkurs Richtungsdetektion
Schwenken der Sende-Antenne mechanisch (Radar) elektrisch (Phased Array Radar)
Interferometrie (Schwenken der Empfangsantenne, Radioastronomie)
Moduliertes Dauerstrichradar (Wikipedia)
Optische Abstandsmessung (Wikipedia)
Homemade phase laser rangefinder (übersetzt)
Homebrew phase laser rangefinder (hackaday.com)
A twofold modulation frequency laser range finder
Bluetooth Direction Finding Fundamentals
UChaser - Ultrasonic Following Control System
Problemstellung
 |
Ein Ultraschallsender T sendet ein Signal aus. Hindernisse Oi im Abstand Xi
im Winkel αi von der Symmetrieachse reflektieren dieses Signal. Zwei Ultraschallempfänger
empfangen das Signal nach unterschiedlichen Zeiten und versetzter Pahsenlage. Bestimme die Xi und αi. |
|||||||||||
 |
Die linke Grafik zeigt das physikalische Modell für ein einzelnes Hindernis.
|
|||||||||||
 |
Ist der Abstand des Hindernisses genügend groß, kann man davon ausgehen, dass die Wellenfronten
nahezu parallel und senkrecht zu X verlaufen. Der hierdurch entstehende
Fehler ist wahrscheinlich deutlich geringer als der, der durch ein nicht punktförmiges reflektierendes
(also ein über mehrere Wellenlängen ausgedehntes) Hindernis entsteht. In diesem Fall gilt: X ≈ A + D / 2 α ≈ arcsin(D / S) |
|||||||||||
 |
In der linken Grafik wurde die Größe von D abgeschätzt. Dazu
wurde das Näherungsmodell genutzt. Die Größenordnung von D liegt in der gleichen Größenordnung wie die üblichen Messgenauigkeit von Ultraschallentfernungsmessgeräten (± ein bis einige cm). D direkt aus der Laufzeitmessung abzuleiten ist nicht möglich. |
Simulation
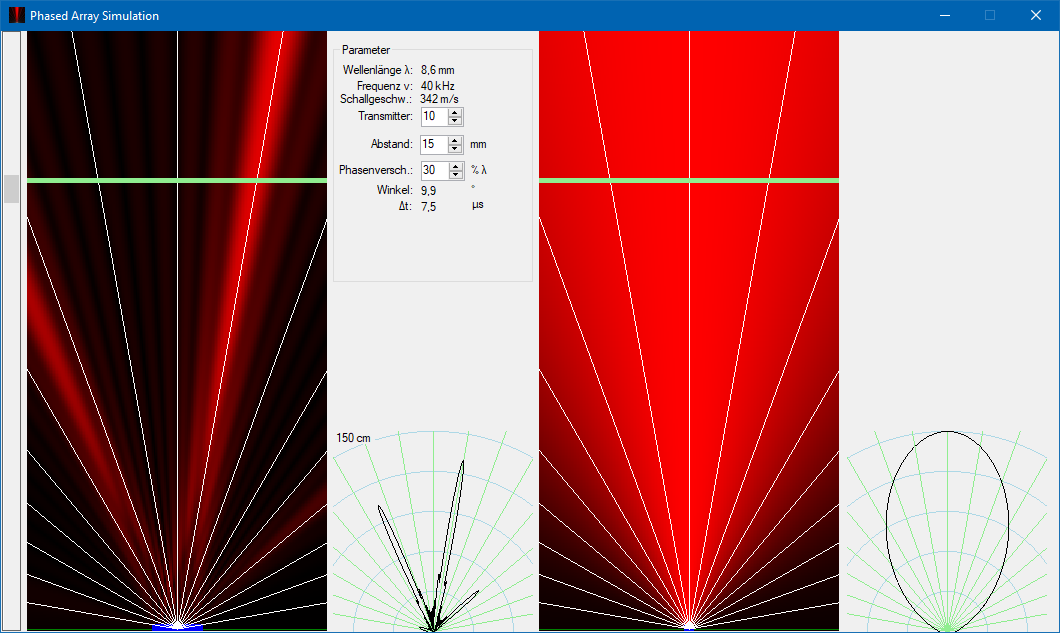
Mit einem kleinen Basic-Programm kann die Richtungsabhängigkeit eines Phased Array simuliert werden.
Arduino Uno?
Geschwindigkeit
Ist es möglich, die Auswertung der Ultraschallempfänger direkt mit einem Arduino vorzunehmen? Das Abtasttheorem besagt, dass die Abtastfrequenz mindestens doppelt so hoch wie die Signalfrequenz sein muss. Das Datenblatt des ATmega328 gibt folgende Auskunft:
- 13 - 260μs Conversion Time
- Up to 76.9kSPS (Up to 15kSPS at Maximum Resolution)
Verzichtet man auf die höchste Genauigkeit von 10 Bit, könnte man das Signal mit fast 77 kHz abtasten. Das ist schon knapp! Bedenkt man weiterhin, dass mindestens zwei Signale gescannt werden müssen wird klar, dass ein einzelner AVR nicht ausreicht. Nutzt man für jedes Signal einen eigenen AVR müssen diese irgendwie synchronisiert werden.
Speicherbedarf
Will man den gesamten Datenstrom speichern, müssen die Scann-Daten für etwa 29 ms (max. Entfernung 5 m) gespeichert werden. Dies bedeutet, dass die Daten von etwa 2300 Samples abgelegt werden müssen. Bei nur 1 Byte pro Sample übersteigt dies die vorhandene Speicherkapazität von 2 KB.
Legt man nur die interessanten Daten ab, also diejenigen, die um den Zeitpunkt des Empfangs des reflektierten Signals herum liegen, müssen Daten für mindestens 200 µs Signaldauer und weitere 150 µs Laufzeitdifferenz abgelegt werden. Insgesamt also für rund 500 µs, entsprechend etwa 40 Byte. Die notwendige Synchronisation zweier Prozessoren ist dadurch aber deutlich aufwendiger, da man sie sich erst im Laufe der Messung darüber einigen können, wann mit der Aufzeichnung der Daten begonnen werden muss.
Fazit: Nahezu nicht machbar!
Die Alternative, z.B. einen ATmega1284 einzusetzen, entschärft zwar die Speicherproblematik, löst aber nicht das Geschwindigkeitsproblem.
STM32F103C8T6
Eine mögliche Alternative zu einem AVR-Prozessor wäre z.B. ein kleines Board auf Basis einer ARM®32-bit Cortex® CPU, das für etwa 5-10 € zu haben ist:
Bluepill, STM32F103C8T6 (ARM®32-bit Cortex®-M3 CPU)
Die relevanten technischen Angaben sind:
- 2 x 12-bit, 1 μs A/D converters (up to 16 channels)
- 20 Kbytes of SRAM
- each ADC shares up to 16 external channels
- The ADC can be served by the DMA controller
Hinzu kommt die Taktfrequenz von 72 MHz, die eine zügige Auswertung auch bei umfangreichen Berechnungen verspricht. Und, für dieses Board gibt es eine Arduino-Bibliothek, so dass man sich nicht mit unbekannten Prozessor-Strukturen herum schlagen muss.
Blackpill, STM32F411CEU6 (ARM®32-bit Cortex®-M4 CPU)
100 MHz (96 MHZ) CPU-Takt, 128KB RAM, 512KB ROM
Zum CPU-Takt: obwohl bei den meisten Boards 100 MHz angegeben wird, haben meine Boards (WeAct V3.0) nur einen Takt von 96 MHz. Der ADC kann bis zu 16 Kanäle mit gut 3 MSPS abtasten.
Messung der Laufzeit-Differenz
Wie bereits oben erwähnt, die Messung der Laufzeit-Differenz auf Basis einer Zeitmessung zu ungenau. Das größte Problem dabei ist, den genauen Zeitpunkt zu bestimmen, zu dem das reflektierte Signal eintrifft.
Alternative
Die Phasenüberlagerung mehrerer Empfänger ist ein extrem aufwändiger Vorgang:
- Man benötigt eine hohe zeitliche Auflösung bei der A/D-Wandlung der Empfangssignale. Erschwinglich sind (Stand Mitte 2021) A/D-Wandler mit 200 ksps. Das sind nur 5 Samples pro Wellenzug und wahrscheinlich deutlich zu wenig.
- Man benötigt relativ viel Speicher um die aufgenommenen Daten zwischen zu speichern. RAM ist bei den meisten μC nur in begrenztem Umfang vorhanden.
- Man benötigt viel Rechenzeit, weil man die empfangenen Daten schrittweise mit verschiedenen Phasenverschiebungen korrelieren muss.
Einfacher scheint der umgekehrte Vorgang. Statt mehrerer Empfänger verwendet man mehrere Sender.
- Dies konzentriert den Ausgangsbeam in eine Richtung.
- Die Richtung kann durch Phasenverschiebung zwischen den Transmittern kontrolliert werden.
Siehe dazu die oben aufgeführte Simulation und auch das Beispiel von Alex Toussaint: How I built an ultrasonic 3d scanner
Beispiel-Konfiguration
Rahmenbedingungen
Mit dem o.a. Simulationsprogramm lässt sich einiges ausprobieren.
Abstand der Transmitter, Winkelabhängigkeit
Mit dem Simulationsprogramm kann man ausprobieren, welche Abstände der Transmitter zu einem konzentrierten Beam führen. Alle Beispiele wurden mit 8 Transmittern berechnet.
 |
 |
 |
| Abstand 10 mm | Abstand 15 mm | Abstand 20 mm |
Durch die Baugröße der Transmitter (MDO-P1040H07T) ist der kleinste Abstand 10 mm (~1,16 λ). Bereits ab einem Abstand von 20 mm (~2,3 λ) nehmen die Neben-Beams beträchtliche Ausmaße an.
Für die Erstellung des Simulationsprogramms wurde die Winkelabhängigkeit des Transmitters ermittelt. Der Schalldruckpegel und damit die Reichweite nimmt relativ schnell ab, wenn man die Hauptrichtung verlässt. Bei etwa 25° beträgt dessen Wert nur noch das 0,7-fache (= 1/√2 ~ -3 dB). Bei 30° ist der Schallpegel bereits auf unter 60% gefallen. Ein sinnvoller Schwenkbereich scheint bei etwa max. ±25° zu liegen.
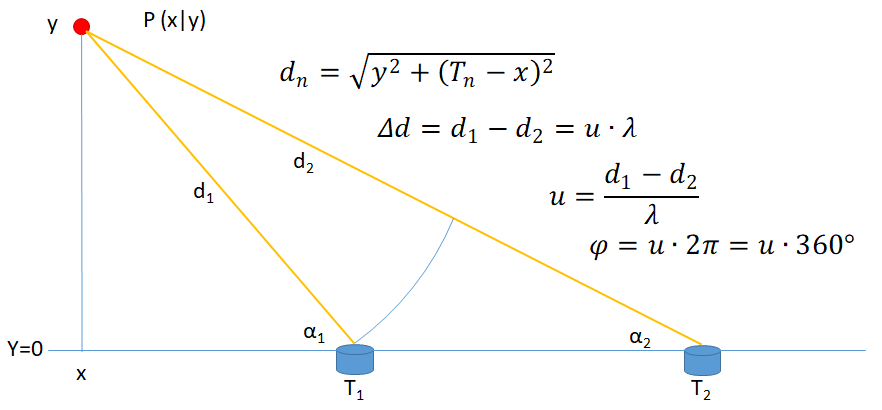
Die Simulation zeigt jedoch, dass dieses Abschätzung deutlich zu optimistisch ist.
Signalgenerierung
Die Erzeugung der phasenverschobenen Signale ist ein exaktes Timing notwendig. Die Resonanzfrequenz der Transmitter und die Phasenverschiebung sollte präzise eingehalten werden können.
Mit der angehängten Excel-Mappe "phased array.xls" lässt sich berechnen, wie groß die zeitliche Verschiebung der Signale zwischen zwei benachbarten US-Transmittern sein muss, um den Beam in eine bestimmte Richtung zu lenken. Hier die Beispielrechnung
| Berechnung der Phasenverschiebung | |||
|---|---|---|---|
| Größe | Wert | Einheit | Erläuterung |
| T | 20 | °C | Lufttemperatur |
| c | 343,1 | m/s | Schallgeschwindigkeit |
| ν | 40 | kHz | benutzte Frequenz |
| λ | 8,578 | mm | Wellenlänge |
| T | 25 | μs | Schwingungsdauer |
| S | 15 | mm | Abstand zweier Transmitter |
| α | 3 | ° | Winkel des Beams |
| Δλ | 0,785 | mm | Phasenverschiebung zwischen benachbarten Transmittern in mm |
| Δt | 2,288 | μs | Phasenverschiebung zwischen benachbarten Transmittern |
| Δt | 2,5 | μs | Phasenverschiebung zwischen benachbarten Transmittern in μs |
| Δλ | 0,858 | mm | Phasenverschiebung zwischen benachbarten Transmittern in mm |
| α | 3,278 | ° | Winkel des Beams |
Eine Verzögerung von 2,5 μs ergibt eine Ablenkung von etwas mehr als 3°. Die Temperaturabhängigkeit ist nicht besonders groß. 3,2° ist ein guter Näherungswert.
| Temperatur | Ablenkung |
|---|---|
| 0°C | 3,16° |
| 10°C | 3,22° |
| 20°C | 3,28° |
| 30°C | 3,33° |
Diese 3° scheint auch als kleinster Schritt sinnvoll zu sein. Eine kleinere Auflösung wird wegen der verbleibenden Unschärfe nicht erreichbar sein. Damit ist man um einiges genauer, als es mit einem einfachen Transmitter möglich wäre. Eine Verschiebung der Signale von 2,5 μs sollte auch mit den üblichen μC erreichbar sein. Die folgende Tabelle listet die Richtungen bei den Mehrfachen von 2,5 μs auf. Die Arkussinus-Funktion ist bei kleinen Werten recht linear. Die Ablenkungswinkel lassen sich deshalb Näherungsweise berechnen durch α = 1,32 °/μs * Δt.
| Δt [μs] |
α [°] |
Δt*1,32 [μs] |
|---|---|---|
| 0 | 0 | 0,0 |
| 2,5 | 3,3 | 3,3 |
| 5,0 | 6,6 | 6,6 |
| 7,5 | 9,9 | 9,9 |
| 10,0 | 13,2 | 13,2 |
| 12,5 | 16,6 | 16,5 |
| 15,0 | 20.0 | 19,8 |
| 17,5 | 23,6 | 23,1 |
| 20,0 | 27,2 | 26,4 |
Die folgende Grafik verdeutlicht die Winkel. Rot markiert ist der ungefähre Erfassungsbereich eines einzelnen Transmitters.
Phasenverschiebung generieren
Die Schwingungsperiode wird in eine gerade Anzahl von Zeitschnitten unterteilt. Gerade Anzahl, damit positive und negative Halbwelle gleich lang sind. Im folgenden Beispiel wird, wie oben beschrieben, die Periode in zehn Schritte zu je 2,5 μs unterteilt. Das folgende kleine Programm erzeugt ein Byte-Array mit den einzelnen Schritten. Die einzelnen Schritte lassen sich dann Timer-gesteuert direkt über einen (Teil-) Port ausgeben.
const int stepsPerPeriod = 10; // Anzahl Schritte pro Periode (2,5us bei 40kHz)
const int channels = 8; // Anzahl Kanäle
const int periods = 4; // Anzahl Wellenzüge die ausgegeben werden sollen
const int maxShift = 5; // Größter Phasenversatz 5 entspricht 16,6°
const int maxSteps = stepsPerPeriod * periods + (channels - 1) * maxShift;
// maxSteps ist 75 bei maxShift = 5 und periods = 4.
uint8_t phaseArray[maxSteps]; // Das Byte-Feld zum Ansteuern der Ports.
// shift: Phasenversatz -maxShift .. +maxShift
void generateArray(int shift) {
bool neg = false;
if (shift < 0) {
neg = true;
shift = -shift;
}
for (int i = 0; i < maxSteps; i++) { // i = Schrittnr.
uint8_t b = 0; // Byte zusammenstellen
for (int channel = 0; channel < channels; channel++) {
bool pin = false;
if ((i - channel * shift >= 0) && (i - channel * shift + 1 <= periods * stepsPerPeriod))
pin = ((i - channel * shift) % 10) < 5;
if (pin)
if (neg)
b += 1 << (channels - 1 - channel);
else
b += 1 << channel;
}
phaseArray[i] = b;
}
}generateArray erzeugt folgende Datensätze:
| generateArray(0) | generateArray(-2) | generateArray(-4) |
| Wellenfront 0° | Wellenfront um 6,6° abgelenkt | Wellenfront um 13,2° abgelenkt |
|
|
|
Ansteuerung der Transmitter
Software
Arduino Uno
Der Arduino Uno (ATmega328p mit 16 MHz CPU-Takt) ist ungeeignet:
- Er besitzt als einzigen komplett herausgeführten 8-Bit-Port den Port D. PD0 und PD1 werden aber für RX und TX benutzt. Die maximale Kanalzahl ist 6 bei Verwendung von Port B.
- Der Arduino Uno ist außerdem zu langsam. Eine minimalistische Timer-ISR könnte so aussehen:
uint8_t phaseArray[maxSteps]; // Das Byte-Feld zum Ansteuern der Ports.
uint8_t arrayIndex = 0;
ISR(TIMER2_COMPA_vect) {
if (arrayIndex < maxSteps)
PORTD = phaseArray[arrayIndex++];
else {
TCCR2B = 0; // Timer stop
TIMSK2 = 0;
}
}Schaut man sich den zugehörigen Assembler-Code an, stellt man fest, dass für die Ausführung dieser Funktion 50 CPU-Zyklen benötigt werden. Bei einer Taktfrequenz von 16 MHz benötigt diese Routine 3,125 μs, also deutlich mehr als die anvisierten 2,5 μs.
| Cycles | Code | |||||
| 5 | ISR-Response 4-5 Zyklen | |||||
| ISR(TIMER2_COMPA_vect) { | ||||||
| 2 | 508: | 1f 92 | push | r1 | ||
| 2 | 50a: | 0f 92 | push | r0 | ||
| 1 | 50c: | 0f b6 | in | r0, 0x3f | ; 63 | |
| 2 | 50e: | 0f 92 | push | r0 | ||
| 1 | 510: | 11 24 | eor | r1, r1 | ||
| 2 | 512: | 8f 93 | push | r24 | ||
| 2 | 514: | ef 93 | push | r30 | ||
| 2 | 516: | ff 93 | push | r31 | ||
| if (arrayIndex < maxSteps) | ||||||
| 2 | 518: | e0 91 1e 01 | lds | r30, 0x011E | ; 0x80011e | |
| 1 | 51c: | eb 34 | cpi | r30, 0x4B | ; 75 | |
| 1 | 51e: | 88 f4 | brcc | .+34 | ; 0x542 | |
| PORTD = phaseArray[arrayIndex++]; | ||||||
| 1 | 520: | 81 e0 | ldi | r24, 0x01 | ; 1 | |
| 1 | 522: | 8e 0f | add | r24, r30 | ||
| 2 | 524: | 80 93 1e 01 | sts | 0x011E, r24 | ; 0x80011e | |
| 1 | 528: | f0 e0 | ldi | r31, 0x00 | ; 0 | |
| 1 | 52a: | e8 5d | subi | r30, 0xD8 | ; 216 | |
| 1 | 52c: | fe 4f | sbci | r31, 0xFE | ; 254 | |
| 2 | 52e: | 80 81 | ld | r24, Z | ||
| 1 | 530: | 8b b9 | out | 0x0b, r24 | ; 11 | |
| else { | ||||||
| TCCR2B = 0; // Timer stop | ||||||
| TIMSK2 = 0; | ||||||
| } | ||||||
| } | ||||||
| 2 | 532: | ff 91 | pop | r31 | ||
| 2 | 534: | ef 91 | pop | r30 | ||
| 2 | 536: | 8f 91 | pop | r24 | ||
| 2 | 538: | 0f 90 | pop | r0 | ||
| 1 | 53a: | 0f be | out | 0x3f, r0 | ; 63 | |
| 2 | 53c: | 0f 90 | pop | r0 | ||
| 2 | 53e: | 1f 90 | pop | r1 | ||
| 4 | 540: | 18 95 | reti | |||
| Gesamt: | 50 | bei 16 MHZ | Dauer: | 3,125 | μs | |
| ISR(TIMER2_COMPA_vect) { | ||||||
| if (arrayIndex < maxSteps) | ||||||
| PORTD = phaseArray[arrayIndex++]; | ||||||
| else { | ||||||
| TCCR2B = 0; // Timer stop | ||||||
| 542: | 10 92 b1 00 | sts | 0x00B1, r1 | ; 0x8000b1> | ||
| TIMSK2 = 0; | ||||||
| 546: | 10 92 70 00 | sts | 0x0070, r1 | ; 0x800070 | ||
| 54a: | f3 cf | rjmp | .-26 | ; 0x532 | ||
Technische Umsetzung
Die Methode des HC-SR04 einen MAX3232 zur Signalverstärkung zu nutzen, scheint eine recht einfache Möglichkeit zu sein. Breakout-Boards mit diesem Chip sind für etwas mehr als 1€ erhältlich. Beim HC-SR04 werden die beiden RS323-Ausgänge im Gegentakt betrieben. Somit liegt die Spannung am US-Transmitter bei etwa ±16 Volt ±8 V (nachgemessen). Damit wird eine Reichweite von 3-4 m erzielt (je nach Lieferant unterscheiden sich die Angaben ein wenig). Für den Nahbereich sollte es ausreichen, mit einem einfachen Takt zu arbeiten. Dann könnten zwei Transmitter mit einem MAX3232 betrieben werden.
Mit einem L239 (2-fach H-Bridge) lassen sich höhere Spannungen erzielen. Die Chips benötigen allerdings eine externe Spannungsquelle in entsprechender Höhe. Mit einem Chip lassen sich zwei Transmitter ansteuern.
Transmitteranzahl, μC-abhängig
Die Port-Breite der meisten μC beträgt 8 Bit. Will man die Schallsignale mit einem μC generieren, bietet es sich an, mit einem Vielfachen von acht Transmitter zu arbeiten. Bei einem Arduino Uno (ATmega328p) stehen sogar nur 2x6 Bits zur Verfügung: PORTB PB0..PB5 und PORTD PD2..PD7 . PD0 und PD1 sind für die serielle Schnittstelle reserviert. Das Ändern von PD1 (= TX) ist unbedingt zu vermeiden. Da die serielle Schnittstelle über Interrupts angesteuert wird, muss außerdem auf Threadsicherheit geachtet werden.
Bei einem ATmega1284 sind alle vier Ports (PORTA..PORTB) verfügbar. Hier lässt sich ein komplett freier 8-Bit-Port finden.
Alternativ bietet es sich an die Signale z.B. von einem ATtiny2313 zu erzeugen. Hier ist ein kompletter Port (PORTB) verfügbar. Der Chip besitzt eine eingebaute USART, mit der er elegant angesteuert werden kann. Alternativ stehen sieben Pins zur Steuerung zur Verfügung.
Andere Möglichkeiten wäre die Benutzung von Schieberegister oder eines i²C-Port-Expanders (z.B. PCF8574). Da hier die Ausgabe seriell erfolgt, müssen entsprechend hohe Taktfrequenzen vorliegen.